NICE: NON-LINEAR INDEPENDENT COMPONENTS ESTIMATION

问题：什么是好的特征表示？（what is a good representation?）非线性的ICA问题。

回答： 好的特征表示能使数据模型更加简单（a good representation is one in which the distribution of the data is easy to model.）

方法： 构造相互独立信号源与可观测数据的可逆映射，与VAE，GAN模型有相似之处，主要与VAE比较。

Model

信号源相互独立：
$$
p_H(h)=\prod_d p_{H_d}(h_d)
$$
假设有可逆映射$f: x \rightarrow h$，那么观察数据的分布为：
$$
p_X(x)=p_H(f(x))|\det(\frac{\partial f(x)}{\partial x})|
$$
生成模型为：
$$ h \sim p_H(h) \\ x = f^{-1}(h) $$
目标函数设置为对数似然，那么主要问题在于雅可比矩阵的行列式计算，下面给出如何构造MLP使雅可比矩阵行列式为1。这个MLP要构造一种特殊的层结构。

Coupling Layer

把$X$按维度切分为两部分$X_{I_1} \in \mathbb R^d, X_{I_2} \in \mathbb R^{D-d}$，分别映射为$Y_{I_1} \in \mathbb R^d,Y_{I_2} \in \mathbb R^{D-d}$
$$ \begin{align} y_{I_1}&=x_{I_1} \\ y_{I_2}&=g(x_{I_2};m(x_{I_1})) \end{align} $$
其中$g: \mathbb R^{D-d} \times m(\mathbb R^d) \rightarrow \mathbb R^{D-d}$，那么计算雅可比矩阵的行列式简化为：
$$ \det \frac{\partial y}{\partial x}= \det \begin{pmatrix} I_d & 0 \\ \frac{\partial y_{I_2}}{\partial x_{I_1}} & \frac{\partial y_{I_2}}{\partial x_{I_2}} \end{pmatrix} $$
逆向有
$$ \begin{align} x_{I_1}&=y_{I_1} \\ x_{I_2}&=g^{-1}(y_{I_2};m(y_{I_1})) \end{align} $$

Additive Coupling Layer

特殊地，如果取$g(a;b)=a+b$，有：
$$ \begin{align} x_{I_1}&=y_{I_1} \\ x_{I_2}&=y_{I_2}-m(y_{I_1}） \end{align} $$
使简化雅可比矩阵的行列式为1：
$$ \det \frac{\partial y}{\partial x}= \det \begin{pmatrix} I_d & 0 \\ \frac{\partial y_{I_2}}{\partial x_{I_1}} & I_{D-d} \end{pmatrix} = 1 $$
如果行列式为1，那么表明映射使保体积不变的，为了避免这种约束，添加缩放因子（有筛选隐变量的作用）。
$$
x_i \rightarrow S_{ii}x_i
$$
这样行列式值为：
$$
\det \frac{\partial y}{\partial x}=
\prod_i S_{ii}
$$

Combing Coupling Layers

叠层增加表达能力。
$$ \begin{align} h_{I_1}^{(1)} &= x_{I_1} \\ h_{I_2}^{(1)} &= x_{I_2}+m^{(1)}(x_{I_1}) \\ h_{I_2}^{(2)} &= h_{I_2}^{(1)} \\ h_{I_1}^{(2)} &= h_{I_1}^{(1)}+m^{(2)}(x_{I_2}) \\ h_{I_1}^{(3)} &= h_{I_1}^{(2)} \\ h_{I_2}^{(3)} &= h_{I_2}^{(2)}+m^{(3)}(x_{I_1}) \\ h_{I_2}^{(4)} &= h_{I_2}^{(3)} \\ h_{I_1}^{(4)} &= h_{I_1}^{(3)}+m^{(4)}(x_{I_2}) \\ h &= exp(s)\odot h^{(4)} \end{align} $$

Loss Function

取最大似然作为优化目标：
$$ \begin{align} \log p_X(x) &= \sum_i \log p_{H_d}(f_d(x))+\log |\det(\frac{\partial f(x)}{\partial x})| \\ &= \sum_i [\log p_{H_d}(f_d(x))+\log |S_{ii}|] \end{align} $$
其中信号源的先验可以取高斯或者logistic分布，取logistic分布在梯度下降方法有更好的表现。

• 高斯分布
  $$
  \log p_{H_d}=-(h_d^2+\log(2\pi))/2
  $$

• logistic分布
  $$
  \log p_{H_d}=-\log(1+\exp(h_d))-\log(1+\exp(-h_d))
  $$

Related Method(NICE, DBM, VAE, GAN)

• DBM

  对数似然难以计算，求解过程梯度运算需要MCMC，耗时一般较长。

• VAE

  使用随机编码器与不完美的解码器，使用ELBO而不是直接优化最大对数似然，这样优化结果可能不是最好的。VAE与DBM都是观测变量在给定隐变量下独立。

• NICE

  使用VAE的基本思想，但是使用确定编码器取代随机编码器。

VI, NF

Variational Inference with Normalizing Flows

问题：如何改进变分推断？

方法：变分推断的一个中心问题就是如何估计后验，在传统的方法中一般使用指数族分布，平均场近似等方法，这样做对变分函数有很大的限制，甚至很难与正确的后验吻合。在这里使用Normalizing Flow的方法使得变分函数具有更强的表达能力与灵活性。

Normalizing Flows, NF

Finite Flows

假设$f:\mathbb R^d \to \mathbb R^d$是可逆映射，$g=f^{-1},z’=f(z)$

$$
q(z’)=q(z)|\det \frac{\partial g}{\partial z’}|=q(z)|\det \frac{\partial f}{\partial z}|^{-1}
$$

通过上面的变换，我们可以由一个分布转换成另外一个分布。如果多次重复上述的变换，可以得到一个分布序列。雅可比行列式可以认为是链式法则。如果把分布想象为一堆粒子，那么可以形象地这一转化过程想象为流。
$$ \begin{align} z_K &= f_K \circ ... \circ f_2 \circ f_1(z_0) \\ \log q_K(z_K) &= \log q_0(z_0)-\sum_{k=1}^K \log |\det \frac{\partial f_k}{\partial z_k}| \end{align} $$
一个有用的性质：

计算流的最终分布的期望可以不用计算雅可比矩阵。

$$
\mathbb E_{q_K}[h(z_K)]=\mathbb E_{q_0}[h(f_K \circ … \circ f_2 \circ f_1(z_0))]
$$

下面具体化映射函数，以及计算雅可比行列式
$$ \begin{align} f(z) &= z+uh(w^Tz+b) \\ \psi(z) &= h'(w^Tz+b)w \\ |\det \frac{\partial f(z)}{\partial z}| &= |\det (\mathbb I+u\psi(z)^T)| = |1+u^T\psi(z)| \end{align} $$
上面的第三条式子式是关键，它表明了特殊形式的变换（称为，Invertible Linear-time Transformation）在计算雅可比行列式上可以有简单的结果。第一条式子形式上比较像残差网络中每一层的变换。
$$ \begin{align} z_K &= f_K \circ ... \circ f_2 \circ f_1(z_0) \\ \log q_K(z_K) &= \log q_0(z_0)-\sum_{k=1}^K \log |1+u_k^T\psi_k(z_k)| \end{align} $$
可逆充分条件 ：并非所以上述形式的映射都是可逆的，要可逆的充分条件是$w^Tu \geq -1$。

证明：

把变量$z$分为平行与垂直于$w$的两部分，即$z=z_{\perp}+z_{|}$，令$h(x)=\tanh(x)$

$$
f(z) = z_{\perp}+z_{|}+uh(w^Tz_{|}+b)
$$
$$ \begin{cases} z_{\|}=\alpha \frac{w}{\| w\|^2} \\ z_{\perp}=y-z_{\|}-uh(w^Tz_{\|}+b) \end{cases} $$
$\alpha$参数要满足下面条件，

$$
w^Tf(z)=\alpha+w^Tuh(\alpha+b)
$$

上式如果关于$\alpha$单调，那么能够推出映射可逆

$$
w^Tu \geq -\frac{1}{h’(\alpha+b)} \geq -1
$$

更特殊地，可以令
$$ \widehat{u}=u+(m(w^Tu)-w^Tu)\frac{w}{\| w\|^2} \\ m(x)=-1+\log(1+\exp(x)) $$

Infinitesimal Flows

与有限流不同，无限流要经过无限次变换。变换过程由偏微分方程描述。

$$
\frac{\partial q_t(z)}{\partial t}=\mathcal T_t[q_t(z)]
$$

Lanevin Flow

粒子运动由随机微分方程（SDE）描述
$$ dz(t)=F(z(t),t)dt+G(z(t),t)d\xi(t) \\ \mathbb E[\xi(t)]=0 \\ \mathbb E[\xi_i(t)\xi_j(t')]=\delta_{ij}\delta(t-t') $$
如果起始的粒子概率分布为$q_0(z)$，经过SDE方程后，概率$q_t(z)$由Fokker-Planck equation描述

$$
\frac{\partial q_t(z)}{\partial t}=-\sum_i \frac{\partial}{\partial z_i}[F_i(z,t)q_t(z)]+1/2\sum_{ij}\frac{\partial^2}{\partial z_i \partial z_j}[D_{ij}(z,t)q_t(z)] \
D=GG^T
$$

在机器学习领域，可以使用$F(z,t)=-\nabla_z \mathcal L(z), G(z,t)=\sqrt(2)\delta_{ij}$，$\mathcal L=\log p(z)$

最终的稳定概率分布为吉布斯分布

$$
q_{\infty}(z)\propto \exp(-\mathcal L)
$$

Hamiltonian Flow

Hamiltonian MC在广义坐标$(z,w)$下可以视为NF

动力学方程

$$
H(z,w)=-\mathcal L(z)+1/2w^TMw
$$

Loss Function

有了上面的等式可以计算VI中最常用的损失函数，ELBO
$$ \begin{align} \mathcal L &= \mathbb E_{q_{\phi}(z|x)}[\log q_{\phi}(z|x)-\log p(x,z)] \\ &= \mathbb E_{q_0(z_0)}[\log q_0(z_0)-\log p(x,z_K)-\sum_{k=1}^K \log |1+u_k^T\psi_k(z_k)|] \\ \end{align} $$

Real NVP

DENSITY ESTIMATION USING REAL NVP

一句话：NICE工作的基础上，构造可逆映射。（偏工程）

real-valued non-volume preserving (real NVP)

Model

可逆映射为：
$$ \begin{cases} y_{I_1}=x_{I_1} \\ y_{I_2}=x_{I_2}\odot \exp(s(x_{I_1}))+t(x_{I_1}) \end{cases} $$ $$ \begin{cases} x_{I_1}=y_{I_1} \\ x_{I_2}=(y_{I_2}-t(y_{I_1}))\odot \exp(-s(y_{I_1})) \end{cases} $$
雅可比行列式：
$$ \det(\frac{\partial y}{\partial x})= \det(\begin{pmatrix} I_d & 0 \\ \frac{\partial y_{I_2}}{\partial x_{I_1}} & diag(\exp(s(x_{I_1}))) \end{pmatrix}) $$

Masked Convolution

b是二值掩膜，可逆映射可以写为下面形式

$$
y = b\odot x + (1-b)\odot(x\odot \exp(s(b\odot x))+t(b\odot x))
$$

IAF

Improved Variational Inference with Inverse Autoregressive Flow

一句话：把可逆映射运用到变分推断中。

具体来说，就是对变分函数进一步具体构造（一个可逆映射），使其具有更强的逼近真实函数（后验概率）的能力。可以认为是NF的特例，工程上比一般的NF更易于实现？

Model

可逆映射为：
$$ z_0 = \mu_0 + \sigma_0 \odot \epsilon, \epsilon\sim \mathcal N(0,\mathbb I) \\ z_t = \mu_t + \sigma_t \odot z_{t-1} $$
雅可比行列式：

$$
\det(\frac{dz_t}{dz_{t-1}})=\prod_{i=1}^D \sigma_{t,i}
$$

流终端的概率分布为：

$$
\log q(z_T|x)=-\sum_{i=1}^D(\epsilon_i^2/2+\log(2\pi)/2+\sum_{t=0}^T \log \sigma_{t,i})
$$

上面的式子可以用于VAE的变分部分。

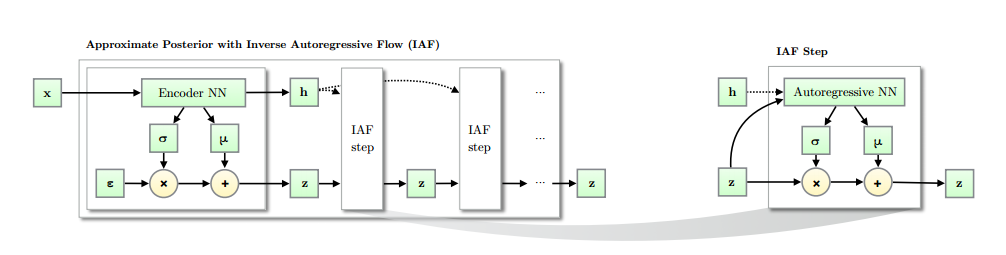
AutoregressiveNN使用了类似LSTM的方法
$$ [m_t,s_t]=AutoregressiveNN_t[z_t,h;\theta] \\ \begin{cases} \sigma_t = sigmoid(s_t) \\ z_t = \sigma_t\odot z_{t-1}+(1-\sigma_t)\odot m_t \end{cases} $$