Sampling
核心问题:如何又快(计算成本低)又好(采样效率高)地采样,一般问题归结为如何计算一个难以解析求解的积分,例如计算后验,期望等。
MC
最古老可以追溯到投针问题,但是现代的MC算法由电子计算机的出现开始广泛使用。
解决解析计算下面的积分十分困难,可以转化为采样估计问题
$$
\mathbb E[f]=\int f(z)p(z)dz
$$
通过一个统计量$\widehat{f}$来估计上面的积分
$$
\widehat{f}=\frac{1}{L}\sum f(z^{(l)})
$$
计算统计量$\widehat{f}$的均值与方差
$$
\mathbb E[\widehat{f}] = \mathbb E[f] \
var[\widehat{f}] = \frac{1}{L} var[f]
$$
上面的方差给出了MC采样的一个重要性质:计算精度与想要估计积分的维度无关,只与采样数量有关。
Basic Sampling
Rejection Sampling
拒绝采样允许我们在更为复杂的分布上做采样。一般地,我们有一个较为简单的分布,在这个分布上采样后根据一个接受率来获得一个样本。具体操作如下:
$p(z)=\widehat{p}(z)/Z$是目标分布,$q(z)$是基准分布,它们满足$\widehat{p}(z) \leq kq(z)$。
- 从基准分布采样,$z_0 \sim q(z)$
- 从均匀分布采样,$u \sim Uniform[0,1]$,如果$u<\frac{\widehat{p}(z)}{kq(z)}$,接受样本$z_0$,否则拒绝样本。
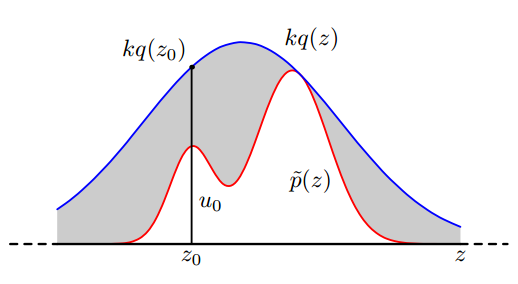
Accepted Ratio
理论上k可以任意,只要满足$\widehat{p}(z) \leq kq(z)$即可。但是由于采样效率的问题,我们希望基准分布与目标分布尽可能贴近。
$$
p(accet)=\int \frac{\widehat{p}(z)}{kq(z)} q(z)dz=\frac{Z}{k}
$$
Adaptive Rejection Sampling
一般的拒绝采样直接从一个单一的基准分布上采样,很多时候基准分布并不能很好地贴近目标分布,可以使用分段的方法。基准分布分成许多小段的指数分布。
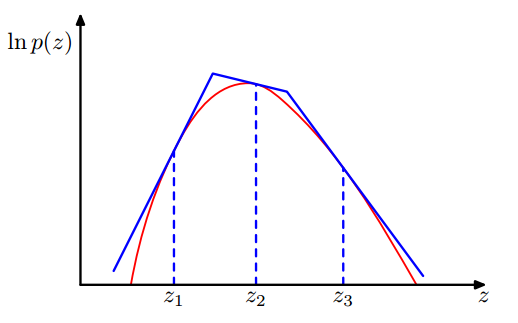
$$
q(z)=k_i\lambda_i
\exp(-\lambda_i(z-z_i) \hspace{10pt } ,z_{i-1} \leq z \leq z_i
$$
Importance Sampling
一般的采样能从目标分布中进行采样,然后再计算积分值(期望等统计量)。重要性采样不能获取目标分布的真实样本,但是可以直接计算积分值。
$$
\begin{align}
\mathbb E[f] &= \int f(z)p(z)dz \\
&= \int f(z)\frac{p(z)}{q(z)}q(z)dz \\
&\approx \frac{1}{L}\sum_{l=1}^L \frac{p(z^{(l)})}{q(z^{(l)})}f(z^{(l)})
\end{align}
$$
考虑没有归一的分布, $p(z)=\widehat{p}(z)/Z_p,q(z)=\widehat{q}(z)/Z_q$
$$
\begin{align}
\mathbb E[f] &= \int f(z)p(z)dz \\
&= \frac{Z_q}{Z_p}\int f(z)\frac{\widehat{p}(z)}{\widehat{q}(z)}q(z)dz \\
&\approx \frac{Z_q}{Z_p}\frac{1}{L}\sum_{l=1}^L \widehat{r}_l f(z^{(l)})
\end{align}
$$
$$
\begin{align}
\frac{Z_p}{Z_q} &= \frac{1}{Z_q} \int \widehat{p}(z)dz \\
&= \int \frac{\widehat{p}(z)}{\widehat{q}(z)}q(z)dz \\
&\approx \frac{1}{L}\sum_{l=1}^L \widehat{r}_l
\end{align}
$$
统一上述的式子
$$
\mathbb E[f] \approx \sum_{l=1}^L w_l f(z^{(l)})
$$
$$
w_l = \frac{\widehat{r}_l}{\sum \widehat{r}_j}
$$
MCMC
Detailed Balance
细致平衡保证分布在特定转移概率下稳定的充分条件(非必须)。数学表述为:
$$
p(z)T(z \to z’)=p(z’)T(z’ \to z)
$$
Metropolis-Hastings algorithm
利用马尔科夫链来进行采样,一个重要概念就是接受概率,与拒绝采样类似,接受概率关系到采样效率。
$$
A(z’,z)=\min(1,\frac{p(z’)q(z|z’)}{p(z)q(z’|z)})
$$
要求转移概率$q(z’|z)$满足遍历性。特殊地,Gibbs算法可以每次转移都有接受概率为1。但是Gibbs算法一帮来说还是收敛很慢。
转移概率的形式可以多种,可以简单地取高斯分布$z’ \sim \mathcal N(z, \sigma^2)$ 。
No Free Lunch
如果考虑转移概率为高斯分布的形式,那么方差大小的选择影响着采样效率。方差太大那么在状态空间转移就快,但是拒绝率也高,导致采样效率并不一定高;方差太小那么在状态空间转移就慢,采样效率一样不高。
Gibbs Sampling
Gibbs采样一般要求目标分布有方便计算的条件概率,状态更新时采样的各个分量交替更新。这既是接受率高同时又是采样效率不高的原因(局域性太强)。
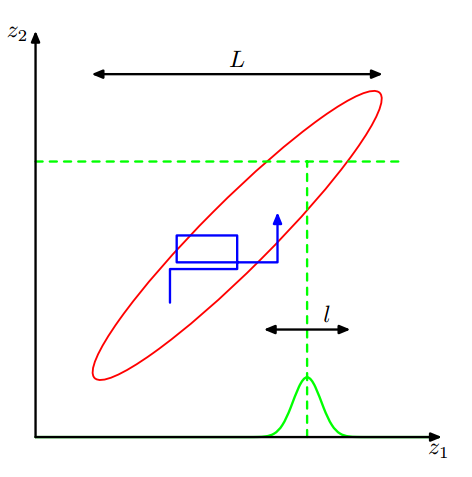
Algorithm
- 初始化$ z_i, i = 1,..,N$
- For t=1,…,T
Sample $z^{t+1}_1 \sim p(z_1|z^t_ 2 ,…,z^t_N)$
Sample $z^{t+1}_2 \sim p(z_2|z^{t+1}_1,x^t_3 ,…,z^t_N)$
…
Sample $z^{t+1}_N \sim p(z_N|z^{t+1} ,…,z^{t+1}_{N-1})$
Hamiltonian MC
一句话:实际上是利用一个动力学过程代替常规MCMC的概率转移过程,这样做可以提高采样效率。
- 首先构造动力学过程,也就是哈密顿量
$$
H(x, p)=K(p)+U(x)
$$
其中$K(p)$代表动能,$U(x)$代表势能,根据哈密顿方程有:
$$
\begin{cases}
\frac{\partial x_i}{\partial t}=\frac{\partial H}{\partial p_i}=\frac{\partial K(p)}{\partial p_i} \\
\frac{\partial p_i}{\partial t}=-\frac{\partial H}{\partial x_i}=-\frac{\partial U(x)}{\partial x_i}
\end{cases}
$$
- 有了哈密顿方程后,可以通过数值方法计算微分方法组,这一步实际上对应常规概率转移的状态更新。
蛙跳更新法(Leap Frog Method)
时间片大小为$\delta$,动量每半步更新一次,位置变量每一步更新一次。
$$
\begin{cases}
p_i(t+\delta/2)=p_i(t)-\delta/2 \frac{\partial U}{\partial x_i(t)} \\
x_i(t+\delta)=x_i(t)+\delta \frac{\partial K}{\partial p_i(t+\delta/2)} \\
p_i(t+\delta)=p_i(t+\delta/2)-\delta/2 \frac{\partial U}{\partial x_i(t+\delta)} \\
\end{cases}
$$
每一次循环,重新采样动量是必要的,因为构造的动力学过程是保守的,也就是说能量守恒。重新采样动量可以防止采样空间不完整。
得到了更新的变量后,还得像常规MCMC算法一样计算接受概率
$$
p(x,p)\propto \exp(-H(x,p))=\exp(-U(x))\exp(-K(p))\propto p(x)p(p)
$$
我们只关心$p(x)$,只要令$U(x)=-\log p(x)$,就可以构造出合适的哈密顿量使我们能够在$p(x)$中采样。
$$
A(x’,p’;x,p) = \min(1,\exp(-U(x’)-K(p’)+U(x)+K(p)))
$$
有了接受概率,其他部分与常规MCMC相同。实际就是用哈密顿动力学过程取代了一个具有遍历性的转移概率。
Algorithm
- $t=0$
- $x^{(0)} \sim \pi^{(0)}$
- 重复直到$t=M$
$t=t+1$
重新采样动量,$p_0 \sim p(p)$
$x_0 = x^{(t-1)}$
用蛙跳法计算新状态$(x’, p’)$,初始值为$(x_0,p_0)$
计算接受率$A(x’,p’;x,p) = \min(1,\exp(-U(x’)-K(p’)+U(x)+K(p)))$
从均匀分布采样,$u \sim Uniform[0,1]$,如果$u \leq A$则接受新状态,$x^{(t)}=x’$, 否则$x^{(t)}=x^{(t-1)}$