Variational Autoencoder
简介
概率模型的问题主要是求解后验或者似然,隐变量的存在使得表达式有可能变得异常复杂。很多时候,后验往往没有解析表达式,或者难以计算。这样使得近似估计成为必不可少的工具。
除了可以使用抽样算法(一般有MCMC,重要性抽样算法等)做估计以外,还可以使用近似推理的方法。
近似推理的核心思想是使用一个较为方便计算的分布去逼近未知的后验或者似然,这里涉及泛函的运算。不过实际上再求泛函极值的时候并非使用一般数学意义的函数空间,而是使用带参数的分布空间,所以问题退化为一般的优化问题。
在深度学习引入后,一般使用深度神经网络来表示这个参数分布。
变分法简介
变分法是处理泛函的数学领域,和处理函数的普通微积分相对。譬如,这样的泛函可以通过未知函数的积分和它的导数来构造。变分法最终寻求的是极值函数:它们使得泛函取得极大或极小值。
变分法的关键定理是欧拉-拉格朗日方程。它对应于泛函的临界点。在寻找函数的极大和极小值时,在一个解附近的微小变化的分析给出一阶的一个近似。它不能分辨是找到了最大值或者最小值(或者都不是)。
变分法在理论物理中非常重要:在拉格朗日力学中,以及在最小作用量原理在量子力学的应用中。变分法提供了有限元方法的数学基础,它是求解边界值问题的强力工具。它们也在材料学中研究材料平衡中大量使用。而在纯数学中的例子有,黎曼在调和函数中使用狄利克雷原理。
同样的材料可以出现在不同的标题中,例如希尔伯特空间技术,莫尔斯理论,或者辛几何。变分一词用于所有极值泛函问题。微分几何中的测地线的研究是很显然的变分性质的领域。极小曲面(肥皂泡)上也有很多研究工作,称为普拉托问题。
来自维基百科
在一般情形下,则需考虑以下的计算式:
$$
A[f]=\int_{x_{1}}^{x_{2}}L(x,f,f’)dx
$$
其中f需有二阶连续的导函数。在这种情形下,拉格朗日量L在极值$f_{0}$处满足欧拉-拉格朗日方程:
$$
\frac{d}{dx}{\frac{\partial L}{\partial f’}}+{\frac{\partial L}{\partial f}}=0
$$
不过在此处,欧拉-拉格朗日方程只是有极值的必要条件,并不是充分条件。
自动编码机
自动编码机主要包括编码器和译码器两部分,一般地编码器和译码器都是神经网络,可以是MLP,CNN,RNN等。
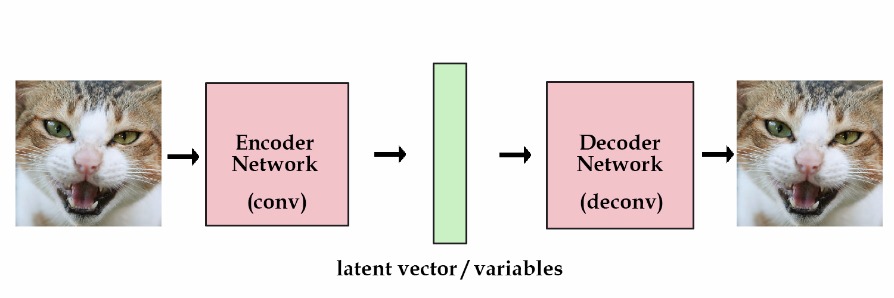
上图给出的就是以卷积神经网络为基础的自动编码机。编码机的目标函数可以为最小均方差MSE,交叉熵或者KL散度等等。其目标是提取自动学习数据特征,得到低维的隐变量(有降维的功能),并且能够重构回原来的数据。它是一种重要的无监督方法,受限玻尔兹曼机是其中著名的一种。
keras在github的博客上有关于各种编码机的简介与实现1 。
变分推理
简单地,考虑一个没有带隐变量的分布$p(x)$,则它的的熵为:
$$
H[p]=\int p(x)\ln p(x)dx
$$
如果以熵为目标函数,那么变分推理可以用到最大熵的方法中去。这在统计物理中最为常见,信息论中也有出现。
如果现在把隐变量$Z$加上,那么
$$
\ln p(X)=\mathcal L(q)+KL[q||p]
$$
其中
$$
\mathcal L(q)=\int q(Z)\ln \frac{p(X,Z)}{q(Z)}dZ
$$
$$
KL(q||p)=\int q(Z) \frac{q(Z)}{q(Z|X)}dZ
$$
其中的 $q(Z)$ 就是我们要设计的分布,与EM算法不同,这里没有显式出现参数,因为它被吸收到我们要设计的分布 $q(Z)$ 中去了。
因为$KL(q||p)\ge0$ ,所以称$\cal L(q)$为$\ln p(X)$的下界,一般我们的任务就是最大化这个下界以达到最大似然的目的。虽然没有直接最大化似然,但是数学上可以证明,极值点处下界与似然重合。不过实际优化一般不可能达到这个极值点,但是这不妨碍它成为实际应用的强大工具。
平均场近似
平均场假设就是多粒子体系中,把体系分成独立的部分,各个部分的相互作用简化为这个部分与它们所有平均得到的场的相互作用。这里是假设隐变量多个变量之间相互独立,可以写成下面的式子:
$$
p(Z)=\prod_{i} p(Z_i)
$$
平均场近似是处理多体物理的重要工具,例如超导理论。不过最近物理学家发现强关联的体系这种方法可能失效。不过我们不关心这个,平均场近似可以使问题化简,剩下的就是相信深度网络可以很好地逼近我们想要的假设。
一些相关的文章
Auto-Encoding Variational Bayes
VAE的结构如下图所示
可以看到其结构与AE很相似,它的隐变量部分假设为独立的高斯分布。
这里一个重要的亮点就是隐变量的抽样部分,与玻尔兹曼机不同,并不需要MCMC,直接高斯分布采样,但是为了满足均值 $\mu$和方差$\sigma^2$的可导性,使用了$Z=\mu+\sigma^2*\epsilon$。要注意的是和图中的z_log_var不同,下面的推导会给出原因。
首先给出对数似然和下界:
$$
\ln p_{\theta}(x^{(1)},…,x^{(N)})=\sum_{i=1}^{N}\ln p_{\theta}(x^{(i)})
$$
$$
\ln p_{\theta}(x^{(i)})=KL(q_{\phi}(z|x^{(i)})||p_{\theta}(z|x^{(i)}))+{\cal L}(\theta,\phi;x^{(i)})
$$
$$
{\cal L}(\theta,\phi;x^{(i)})=\int q_{\phi}(z|x^{(i)})\ln \frac{p_{\theta}(x^{(i)},z)}{q_{\phi}(z|x^{(i)})}dz
$$
这里与变分推理的基本分解方法相同,就等着优化下界$\cal L$。
把下界再分解为两部分,简化起见$x^{(i)}\to x$
$$
{\cal L}(\theta,\phi;x)=\mathbb{E}_{q_{\phi}(z|x)}[-\ln q_{\phi}(z|x)+\ln p_{\theta}(x,z)]
$$
再次重写为:
$$
{\cal L}(\theta,\phi;x)=-KL(q_{\phi}(z|x)||p_{\theta}(z))+\mathbb{E}_{q_{\phi}(z|x)}[\ln p_{\theta}(x|z)]
$$
到这里已经得到目标函数的解析形式,剩下的就是积分简化和抽样估计。注意到$q_{\phi}(z|x)$和$p_{\theta}(x|z)$分别就是编码器与译码器,它们都用神经网络来设计,$\phi$是变分参数而$\theta$是生成参数。
KL散度在隐变量为独立高斯分布时可以化简
$$
\begin{aligned}
\int q_{\phi}(z)\ln p(z)dz&=\int{\cal N}(z;\mu,\sigma^2)\ln {\cal N}(z;0,\mathbb{I}) \\
&=-\frac{J}{2}\ln(2\pi)-\frac{1}{2}\sum_{j=1}^{J}(\mu_j^2+\sigma_j^2)
\end{aligned}
$$
$$
\begin{aligned}
\int q_{\phi}(z)\ln q_{\phi}(z)dz&=\int {\cal N}(z;\mu,\sigma^2)\ln {\cal N}(z;\mu,\sigma^2)dz \\
&=-\frac{J}{2}\ln(2\pi)-\frac{1}{2}\sum_{j=1}^{J}(1+\ln\sigma_j^2)
\end{aligned}
$$
有了上面的式子就可以得到KL散度的表达式:
$$
{-KL(q_{\phi}(z)||p_{\theta}(z))=\frac{1}{2}\sum_{j=1}^{J}(1+\ln\sigma_j^2-\mu_j^2-\sigma_j^2)}
$$
在这里可以介绍上文结果图中z_log_var出现的原因了,因为直接用神经网络来学习$\ln\sigma^2$ 然后$\sigma^2=\exp(\ln \sigma^2)$比较方便,$\exp()$比$\ln()$要好。
第二部分可以写为:
$$
\mathbb{E}_{q_{\phi}(z)}[p_{\theta}(x|z)]\approx\frac{1}{L}\sum_{l=1}^{L}p_{\theta}(x|z^{(l)})
$$
$$
z^{(l)}\sim q_{\phi}(z|x)
$$
综合上面的式子可以得到下界的估计,把$x\to x^{(i)}$换回来
$$
{\cal L}(\theta,\phi;x^{(i)})=\frac{1}{2}\sum_{j=1}^{J}(1+\ln\sigma_j^{(i)2}-\mu_j^{(i)2}-\sigma_j^{(i)2})+\frac{1}{L}\sum_{l=1}^{L}p_{\theta}(x^{(i)}|z^{(i,l)})
$$
有了目标函数,只要对其做导数就可以Update参数了。
注意MC取样对$\phi$的梯度估计为:
$$
\nabla_{\phi}\mathbb{E}_{q_{\phi}(z)}[f(z)]=\mathbb{E}_{q_{\phi}(z)}[f(z)\nabla_{\phi}\ln q_{\phi}(z)]\approx\frac{1}{L}\sum_{l=1}^{L}f(z^{(l)})\nabla_{\phi}\ln q_{\phi}(z^{(l)})
$$
$$
z^{(l)}\sim q_{\phi}(z|x)
$$
A Tutorial on Variational Bayesian Inference tedious
这篇文章主要推导了平均场下的变分推理和Variational Message Passing(VMP)框架的简单介绍。
遵循文章中的记号,推导平均场下的变分推理。
$D$是数据或者可视变量,$x$是隐变量,$Q(x)$是近视分布,$\theta$是参数。
$$
Q(x)=\prod_iQ_i(x_i)
$$
$$
\forall i,\int dx_iQ_i(x_i)=1
$$
$Q(x)$要逼近$P(x|D)$,给出$KL$散度:
$$
KL(Q(x)||P(x|D))=\int dxQ(x)\ln\frac{Q(x)}{P(x|D)}
$$
与变分推理的基本分解相同,得到表达式:
$$
P(D)=L[Q(x)]+KL(Q(x)||P(x|D))
$$
$$
L[Q(x)]=\int dxQ(x)\ln\frac{P(x,D)}{Q(x)}
$$
接下来分解$L[Q(x)]$
$$
\begin{aligned}
L[Q(x)] &=\int dxQ(x)\ln\frac{P(x,D)}{Q(x)} \\
&=\int dxQ(x)\ln P(x,D)-\int dxQ(x)\ln Q(x) \\
&=\langle E(x,D)\rangle_{Q(x)}+H[Q(x)] \\
\end{aligned}
$$
这里分成了能量和熵两部分,物理上能量更喜欢用$P\propto\exp(-\frac{E}{T})$,带符号。
加入平均场假设,熵化简为:
$$
H[Q(x)]=\sum_i\int dx_iQ_i(x_i)\ln Q_i(x_i)
$$
能量部分写为,$Z$是配分函数,是常数:
$$
\begin{aligned}
\langle E(x,D)\rangle_{Q(x)}&=\int dx_i Q_i(x_i)\langle E(x,D)\rangle{Q(\bar x_i)} \\
&=\int dx_iQ_i(x_i)\ln Q_i^*(x_i)+\ln Z
\end{aligned}
$$
$$
Q_i^{\star}(x_i)=\frac{1}{Z}\exp(\langle E(x,D)\rangle_{Q(\bar x_i)}),{x_i,\bar x_i}
$$
合并后得到
$$
L[Q(x)]=-KL(Q_i(x_i)||Q_i^*(x_i))+H[Q_i(\bar x_i)]+\ln Z
$$
变分求导得到:
$$
\frac{\delta}{\delta Q_i(x_i)}{-KL(Q_i(x_i)||Q_i^*(x_i))-\lambda_i(\int Q_i(x_i)dx_i)-1}=0
$$
得到极值条件:
$$
Q_i(x_i)=Q_i^{\star}(x_i)
$$
$$
Q_i(x_i)=\frac{1}{Z}\exp(\langle E(x,D)\rangle_{Q(\bar x_i)})
$$
观察上面式子的形式可以得到一个马尔科夫链($\bar x_i \rightarrow x_i \rightarrow \bar x_i^* \rightarrow …$),这种坐标迭代的方法与Gibbs采样算法有很强的联系。
Variational Message Passing
VMP最终目标就是要把人们从冗余的推导中解放出来,使用了信息传递模型,信息分为两类,一种是natural parameter vector(子节点到父节点)和vector of moment(父节点到子节点)。以指数族分布作为信息传递,这个很重要,因为指数族分布可以使用共轭分布的重要特征(先验分布与后验分布同是指数族分布)。
$$
P(X)=\prod_i P(X_i|{Pa}_i)
$$
这个是贝叶斯网络的一个重要公式,联合分布总是可以分解为子节点与父节点条件概率的乘积。
回到平均场近似讨论的部分
$$
Q_i^{\star}(x_i)=\frac{1}{Z}\exp(\langle E(x,D)\rangle_{Q(\bar x_i)})
$$