Post-Nonlinear Independent Component Analysis by Variational Bayesian Learning

问题：解决非线性的盲源分离问题。

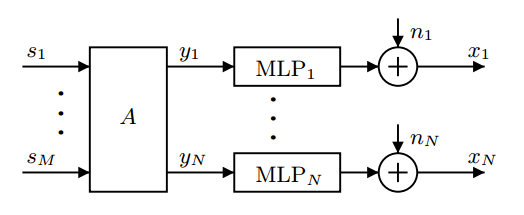
方法：模型使用链接矩阵$A$表达线性叠加部分，MLP表达非线性部分。变分贝叶斯方法（VB）做推断，梯度下降求解。

Model

$$
x_i(t)=f_i[\sum_{j=1}^Ma_{ij}s_j(t),W_i]+n_i(t)
$$
$x_i(t)$是可观测数据，$s_i(t)$是独立信号源，$f_i[*,W_i]$代表MLP，$n_i$是独立噪声

Loss Function

ELBO作为优化目标，过程与VAE十分相似。
$$ \begin{align} \mathcal L &=\mathbb E_{q(S,\theta)}[\log\frac{q(S,\theta)}{p(S,\theta,X)}] \\ &=\mathbb E_{q(S,\theta)}[\frac{q(S,\theta)}{p(S,\theta)}]-\mathbb E_{q(S,\theta)}[p(X|S,\theta)] \end{align} $$
$$
p(X|S,\theta)=\prod_{i,t}\mathcal N(x_i(t);f_i[\sum a_{ijs_j(t)},W_i],\sigma_i^2)
$$