Basic Concept

Qubit

一位量子比特可以表示为$|0\rangle,|1\rangle$态的叠加，记为：

$$ |\psi\rangle = \alpha|0\rangle+\beta|1\rangle \\ |\alpha|^2+|\beta|^2=1 \\ \alpha = \cos \frac{\theta}{2} \\ \beta = e^{i\phi}\sin \frac{\theta}{2} $$

用线性代收的记号来表示可以记为：

$$ |0\rangle = {\bigl [}{\begin{smallmatrix}1\\0\end{smallmatrix}}{\bigr ]} \\ |1\rangle = {\bigl [}{\begin{smallmatrix}0\\1\end{smallmatrix}}{\bigr ]} \\ |\psi\rangle = {\bigl [}{\begin{smallmatrix}\cos \frac{\theta}{2}\\e^{i\phi}\sin \frac{\theta}{2}\end{smallmatrix}}{\bigr ]} $$

一个量子比特可以直观地表示为一个Bloch球。

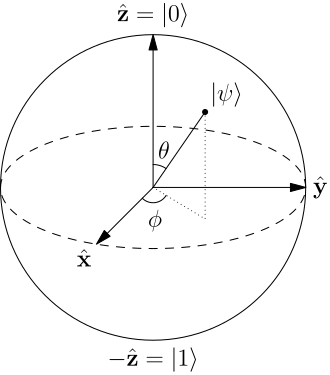
多位量子比特的态没有这种直观的可视图，一般表示为：

$$ |\psi\rangle = \sum_{i=0}^{2^n-1}c_i|i\rangle $$

Quantum logic gate

单比特门

• Hadamard (H) gate

$$ H = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} $$

• Pauli-X gate (= NOT gate)

$$ X = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} $$

• Pauli-Y gate

$$ Y = \begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix} $$

• Pauli-Z ($R_{\pi }$) gate

$$ Z = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} $$

• Phase shift ($R_{\phi }$) gates

$$ R_{\phi }=\begin{bmatrix}1&0\\0&e^{i\phi }\end{bmatrix} $$

双比特门

• Controlled gates

$$ {\mbox{CNOT}}= cX={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{bmatrix}} $$

Solovay–Kitaev定理：任何量子门可以由一组较少的量子门（只需包含单比特与双比特门）有效逼近。

例如包括$H, \ R_{Z}(\pi /4),\ CNOT$这三个门的集合。

Measure

测量会导致量子态塌缩，至于塌缩到哪个态与测量基有关，测量基相互正交。一般测量基为${|i\rangle |i=0…2^n-1}$。

若$|\psi\rangle = \sum_{i=0}^{2^n-1}c_i|i\rangle$，那么塌缩到$|i\rangle$的概率$\Pr(i) = |c_i|^2$。

Quantum Algorithm

量子算法基本步骤:

1. 配置初始态，一般为$|0\rangle ^{\otimes n}$。
2. 对量子比特操作一系列的量子门。
3. 对量子比特进行测量，记录测量结果（经典信息）。
4. 也许有必要根据步骤3的结果再次进行步骤2。

对于量子分支控制还没有定论，根据步骤4这种方法进行分支控制这与经典的方法很相似。

Deutsch–Jozsa algorithm

问题：函数$f:{0,1}^n \to {0,1}$，判断函数是常数还是平衡的（一半是0，一半是1）。假定函数只能是其一。

要正确做出判断，经典算法最坏需要进行$2^{n-1}+1$计算。量子算法只需要一次就可以完成。

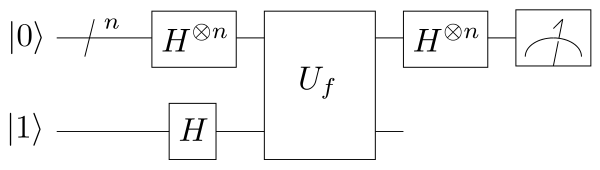
算法步骤：

1. 初始态为$|0\rangle ^{\otimes n}|1\rangle $，执行门$H^{\otimes n},\ H$后为：

$$ {\frac {1}{{\sqrt {2^{{n+1}}}}}}\sum _{{x=0}}^{{2^{n}-1}}|x\rangle (|0\rangle -|1\rangle ) $$

假设函数$f$是个黑盒，称为量子神谕（quantum oracle），记为$U_f$。它的实现$|x\rangle |y\rangle \to |x\rangle |y\oplus f(x)\rangle $的映射。

1. 继续执行门$U_f$得到：

$$ {\frac {1}{{\sqrt {2^{{n+1}}}}}}\sum _{{x=0}}^{{2^{n}-1}}|x\rangle (|f(x)\rangle -|1\oplus f(x)\rangle ) = {\frac {1}{{\sqrt {2^{{n+1}}}}}}\sum _{{x=0}}^{{2^{n}-1}}(-1)^{{f(x)}}|x\rangle (|0\rangle -|1\rangle ) $$

1. 对前面的$n$个比特操作门$H^{\otimes n}$，现在可以不考虑最后一个比特。得到：

$$ {\frac {1}{2^{n}}}\sum _{{x=0}}^{{2^{n}-1}}(-1)^{{f(x)}}\left[\sum _{{y=0}}^{{2^{n}-1}}(-1)^{{x\cdot y}}|y\rangle \right]={\frac {1}{2^{n}}}\sum _{{y=0}}^{{2^{n}-1}}\left[\sum _{{x=0}}^{{2^{n}-1}}(-1)^{{f(x)}}(-1)^{{x\cdot y}}\right]|y\rangle \\ x\cdot y=x_{0}y_{0}\oplus x_{1}y_{1}\oplus \cdots \oplus x_{{n-1}}y_{{n-1}} $$

1. 测量前面$n$个比特，得到态$|0\rangle ^{\otimes n}$的概率为：

$$ {\bigg |}{\frac {1}{2^{n}}}\sum _{{x=0}}^{{2^{n}-1}}(-1)^{{f(x)}}{\bigg |}^{2} $$

也就是说如果函数是常数我们得到态$|0\rangle ^{\otimes n}$的概率为1，函数是平衡则为0。

Grover’s Algorithm

也成为量子搜索算法。

问题：黑盒函数$f$只有一个输入的输出值与其它输入不，输入域大小为$N$，如何快速找出该特定的输入。

经典算法复杂度为$O(N)$，量子算法复杂度为$O(\sqrt{N})$。

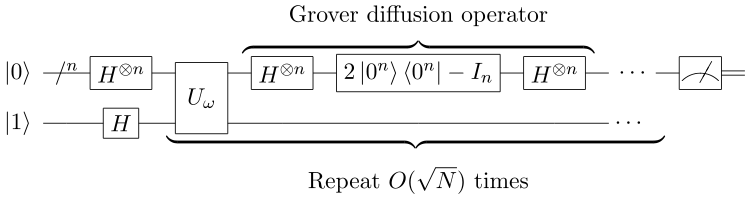
函数的量子神谕$U_{\omega}$实现的映射是：

$$ {\begin{cases}U_{\omega }|x\rangle =-|x\rangle &{\text{for }}x=\omega {\text{, that is, }}f(x)=1,\\U_{\omega }|x\rangle =|x\rangle &{\text{for }}x\neq \omega {\text{, that is, }}f(x)=0.\end{cases}} $$

算法步骤：

1. 初始态为$|0\rangle ^{\otimes n}|1\rangle $，执行门$H^{\otimes n}$后为：

$$ |s\rangle ={\frac {1}{\sqrt {N}}}\sum _{x=0}^{N-1}|x\rangle $$

1. 操作Grover算子，重复$\sqrt{N}$次。$G=U_{\omega}U_{s}$

$$
U_{s}=2\left|s\right\rangle \left\langle s\right|-I
$$

1. 测量将以概率$\sin ^{2}\left({\Big (}\sqrt{N}+{\frac {1}{2}}{\Big )}\theta \right)$得到正确答案。

• 几何解释

$$ |s \rangle = \frac{1}{\sqrt{N}}|\omega \rangle + \frac{\sqrt{N-1}}{\sqrt{N}}|s' \rangle \\ |s' \rangle = \frac{1}{\sqrt{N-1}}\sum_{x\neq \omega}|x \rangle \\ \sin {\frac {\theta }{2}}={\frac {1}{\sqrt {N}}} $$

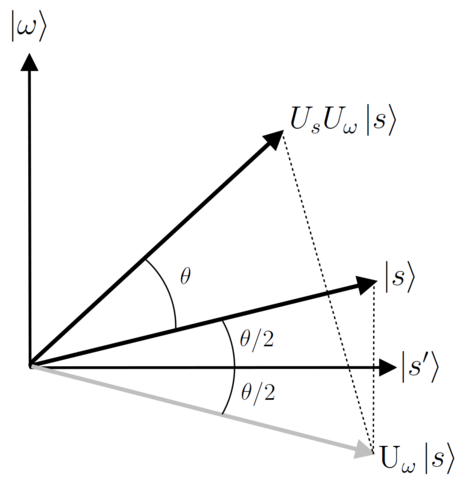
Grover算子可以认为是$\omega \rangle,|s’ \rangle$张成的平面上转角$\theta$的算子。整个流程可以认为是振幅放大的过程。

Quantum Fourier Transform

$$
QFT:|x\rangle \mapsto {\frac {1}{\sqrt {N}}}\sum _{k=0}^{N-1}\omega _{n}^{xk}|k\rangle \
\omega _{n}=e^{\frac {2\pi i}{N}}
$$

Quantum Phase Estimation Algorithm

问题：酉算子$U$有本征态$|\psi \rangle$，满足$U|\psi \rangle =e^{2\pi i\theta }\left|\psi \right\rangle ,0\leq \theta <1$，估计相位$\theta$。

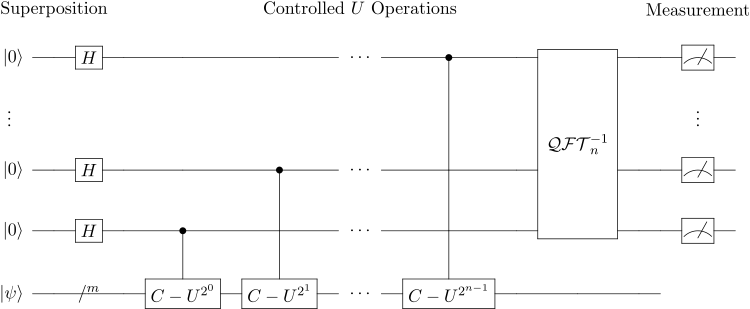
把量子比特分成两大部分，第一寄存器存放相位估计的结果，第二寄存器用于存放待估计算子的本态。

算法步骤：

1. 初始态为$|0\rangle ^{\otimes n}|1\rangle $，执行门$H^{\otimes n}$。

2. 操作一系列$C-U$门，它是一种控制门。它的功能是当控制比特为1时，受控比特进行$U$门操作。
   得到第一寄存器的量子态为：

$$ {\frac {1}{2^{\frac {n}{2}}}}\underbrace {\left(|0\rangle +e^{2\pi i2^{n-1}\theta }|1\rangle \right)} _{1^{st}\ qubit}\otimes \cdots \otimes \underbrace {\left(|0\rangle +e^{2\pi i2^{1}\theta }|1\rangle \right)} _{n-1^{th}\ qubit}\otimes \underbrace {\left(|0\rangle +e^{2\pi i2^{0}\theta }|1\rangle \right)} _{n^{th}\ qubit}={\frac {1}{2^{\frac {n}{2}}}}\sum _{k=0}^{2^{n}-1}e^{2\pi i\theta k}|k\rangle $$

1. 对第一寄存器进行逆QFT。
   得到第一寄存器的量子态为：

$$ {\frac {1}{2^{n}}}\sum _{x=0}^{2^{n}-1}\sum _{k=0}^{2^{n}-1}e^{2\pi i\theta k}e^{\frac {-2\pi ikx}{2^{n}}}|x\rangle ={\frac {1}{2^{n}}}\sum _{x=0}^{2^{n}-1}\sum _{k=0}^{2^{n}-1}e^{-{\frac {2\pi ik}{2^{n}}}\left(x-2^{n}\theta \right)}|x\rangle $$

所有寄存器的量子态为：

$$ {\frac {1}{2^{n}}}\sum _{x=0}^{2^{n}-1}\sum _{k=0}^{2^{n}-1}e^{-{\frac {2\pi ik}{2^{n}}}\left(x-2^{n}\theta \right)}|x\rangle \otimes |\psi \rangle = {\frac {1}{2^{n}}}\sum _{x=0}^{2^{n}-1}\sum _{k=0}^{2^{n}-1}e^{-{\frac {2\pi ik}{2^{n}}}\left(x-a\right)}e^{2\pi i\delta k}|x\rangle \otimes |\psi \rangle \\ 2^{n}\theta =a+2^{n}\delta ,\ 0\leqslant |2^{n}\delta |\leqslant {\tfrac {1}{2}} $$

1. 对第一寄存器测量得到相位估计值$a$的概率为$\Pr(a)$。

$$ \Pr(a)=\left|\left\langle a\underbrace {\left|{\frac {1}{2^{n}}}\sum _{x=0}^{2^{n}-1}\sum _{k=0}^{2^{n}-1}e^{{\frac {-2\pi ik}{2^{n}}}(x-a)}e^{2\pi i\delta k}\right|} _{\text{State of the first register}}x\right\rangle \right|^{2}={\frac {1}{2^{2n}}}\left|\sum _{k=0}^{2^{n}-1}e^{2\pi i\delta k}\right|^{2}={\begin{cases}1&\delta =0\\&\\{\frac {1}{2^{2n}}}\left|{\frac {1-{e^{2\pi i2^{n}\delta }}}{1-{e^{2\pi i\delta }}}}\right|^{2} \geq \frac{4}{\pi^2} &\delta \neq 0\end{cases}} $$

这种相位估计是近似的，要提高精度要消耗比特位。增加测量概率为$1-\epsilon$，需要比特数$O(\log(1/\epsilon )$。

Quantum Counting Algorithm

问题：函数$f:{0,1}^n \to {0,1}$，问题的解集为$B$。函数是一个指示函数，满足：
$$ f(x)={\begin{cases}1&x\in B\\0&x\notin B\end{cases}} $$
现在要计算解集的大小$M=|B|$。

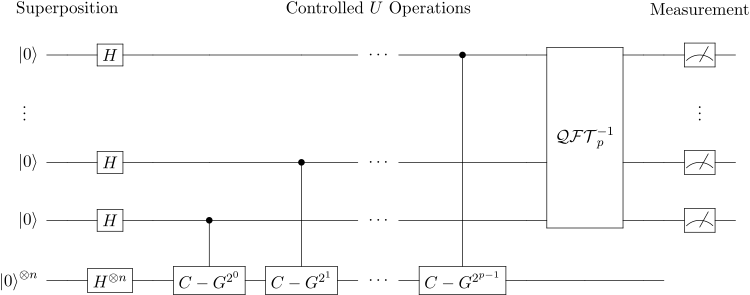
算法步骤与相位估计算法相同，不过是把待估计的算子具体化为Grover算子。是Grover算法与相位估计算法的结合。
由前面讨论可以知道Grover算子是一个转动矩阵，可以表示为：

$$ G={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}} $$

它的本证值为$e^{\pm i\theta }$。

$M$的估计为：

$$ \sin {\frac {\theta }{2}}={\sqrt {\frac {M}{N}}} \\ {\frac {\vert \Delta M\vert }{N}}=\left\vert \sin ^{2}\left({\frac {\theta +\Delta \theta }{2}}\right)-\sin ^{2}\left({\frac {\theta }{2}}\right)\right\vert $$

• Quantum existence problem

如果只关心$M$是否为0，而不关心具体值，那么较低精度的相位估计也可以接受。

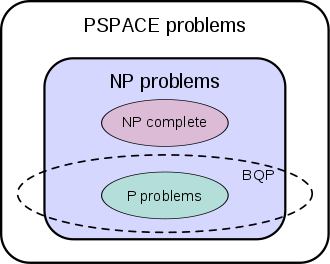
bounded-error quantum polynomial time,BQP

BQP是一个很重要的量子算法复杂类，这类判断问题能够被量子计算机在多项式时间（量子门序列长度为多项式）内判断，并且正确率大于$\frac{2}{3}$。

形式化语言描述：

语言$L$在BQP内当且仅当存在多项式时间的量子线路${Q_n|n\in \mathbb N}$，使得满足下列条件：

• $\forall n \in \mathbb N$，量子线路输入$n$个量子比特，输出一个经典比特
• $\forall x \in L, \Pr(Q_{|x|}=1)\geq 2/3$
• $\forall x \notin L, \Pr(Q_{|x|}=0)\geq 2/3$

理想的复杂类的包含关系（有争议的）：